Introdução
Bom dia, boa tarde e boa noite, esse post sai um pouco da temática de front-end, mas é um tópico muito útil para quem acaba topando com sistemas de delivery, onde o usuário é o centro das atenções e precisa ser informado das opções disponíveis a sua volta.
Descobrir se um ponto está dentro de um circulo é algo muito fácil de se fazer, tendo o raio(maior distancia aceitavel do centro), você só precisa calcular a distancia entre o centro e ponto seguindo fórmula
D=sqrt((Xo-X)²+(Yo-Y)²) e comparar a distancia com o raio, sendo menor aquele ponto estará dentro do aceitável.
Tudo muito bonito, você calcular um a um dentro de um DB com 100 inserções, mas e quando seu DB tiver 100mil pontos? Calcular um a um se torna um processo custoso, caso vá fazer isso a toda requisição do usuário.
Sendo assim, vamos ver o que podemos fazer para aprimorar essa pesquisa.
Não é somente a hipotenusa
Infelizmente, tenho que lhe contar a verdade, aquele calculo de D acima não adiantará para você, aquele calculo é ideal em um plano cartesiano simples, o que não é o caso da terra que é uma esfera. Sendo assim a menor distância entre dois pontos será definida pela Ortodromia.
Dado dois pontos A(latA, longA) e B(latB, longB) nós calculamos a distancia entre eles com a seguinte fórmula:
D = arccos(sin(latA)*sin(latB) + cos(latA)*cos(latB)*cos(longA - longB))*Raio
-- dado uma origem em O=(1.3963 rad, -0.6981 rad) latitude e longitude
-- temos nossa primeira query ao banco de dados em um raio de 300 km
SELECT * FROM LOCAIS WHERE acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) * 6371 <= 300;
A nossa query está feita, porém existe mais um problema, ela não utilizará o poder dos índices pois as operações envolvendo latitude e longitude são muito complexas. Dessa forma nosso processamento será lento e muito custoso ao usuário.
Índices em Lat e Long
Podemos adicionar índices no campo de latitude e longitude da nossa tabela `LOCAIS` e utilizar uma bounding box para diminuir ao máximo o número de locais possíveis.
Bounding box é nada menos que o menor retângulo possível que cubra toda a nossa forma geométrica(sim, a bounding box não é exclusivo para retangulos), abaixo segue uma imagem de exemplo do que seria uma bounding box em um circulo.

A bounding box é toda a área em azul, é o retângulo que possui toda a totalidade do círculo. Aplicando-a ao nosso problema, nós buscariamos todos os pontos que estivessem entre ymin/ymax e xmin/xmax, dessa forma conseguiriamos reduzir a quantidade de pontos a um numero muito menor do que a imensidão que pode ser nosso banco de dados, e o cálculo complexo será executado menos vezes.
Definindo a Latitude min/max
Agora é a parte que começa a complicar um pouco a explicação caso você não manje muito geometria analítica.
Utilizando ainda os números do exemplo anterior, vamos definir nosso raio de busca em D = 300km e raio da terra(aproximadamente) R = 6371km.
r = D/R = (300km/6371km) = 0.0471 rad
Esse r que conseguimos, é o raio da nossa busca em forma angular, assim podemos somar/subtrair essa distancia da nossa latitude para obter a Latmax e Latmin, nada mais do que obter os extremos do nosso círculo.
Latmin = Lat - r = (lat - D/R)
Latmax = Lat + r = (lat + D/R)
Definindo a Longitude min/max
Ao contrário da latitude, o raio da terra é alterado, conforme mostrado na figura abaixo, no sentido longitudinal baseado na atual latitude, dessa forma a mesma diferença de distância entre dois angulos em latitudes diferentes podem ter distancias diferentes.
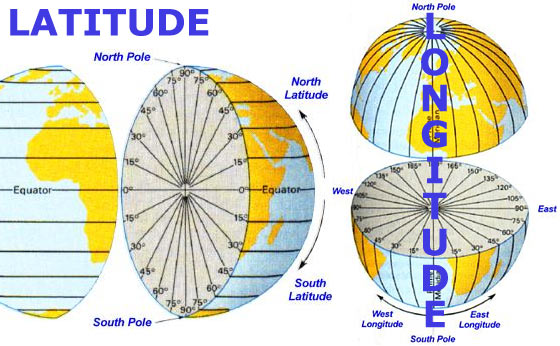
Abaixo tem outra imagem com uma melhor visualização do nosso problema, nossa longitude min/max será T1 e T2, dessa forma não deixaremos um pedacinho do círculo para fora, na hora que a distancia entre as longitudes afina subindo a latitude.
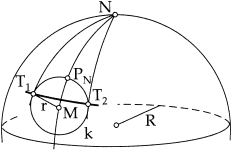
Para calcular essa diferença angular, que necessitaremos adicionar a nossa conta, além da distância r calculada no último tópico. Utilizaremos as seguintes fórmulas, retiradas do livro.
latT = arcsin(sin(lat)/cos(r)), latT é a latitude que subimos a linha mais escura em relação ao meio.
Δlon = arccos((cos(r)-sin(latT)*sin(lat))/(cos(latT)*cos(lat)))
Δlon = arcsin(sin(r)/cos(lat)), simplificando com algumas propriedades trigonométricas a equação acima, temos essa.
Por fim, a longitude min/max, será calculada por:
Lonmin = lonT1 = Lon - Δlon
Lonmax = lonT2 = lon + Δlon
Pólos e o Meridiano de 180º
A latitude é dividida em 4 intervalos de π/2, ou seja, toda vez que esse limite +-π/2 é ultrapassado, isso significa que um dos polos está no nosso raio, se positivo é o polo norte, se negativo é o polo sul.
Pra resolver esse problema caso a Latmax > π/2, Latmax = π/2, e se Latmin < -π/2, Latmin = -π/2.
O problema na longitude é semelhante, como ela é dividida em dois intervalos de π. Caso fizessemos como na latitue e simplesmente definir limites aos valores dessa variável, como Lonmin < -π, Lonmin = -π, nós iriamos fazer uma bounding box que mais parece um cinto em volta da terra, assim acabariamos incluindo muitos pontos possíveis desnecessários.
A forma ideal de resolver o problema é criando duas bounding box diferentes, uma que vai pegar checar em um lado do meridiano de 180º e outra que irá chegar o outro lado.
Dessa forma, caso Lonmin < -π, nossas duas bounding box serão formadas pelos pontos (Latmin, Lonmin+2π):(Latmax, π) e (Latmin, -π):(Latmax, Lonmax).
E Lonmax > π, (Latmin, Lonmin):(Latmax, π) e (Latmin, -π):(Latmax, Lonmax-2π).
Dando uma pincelada novamente nessa parte da longitude. O que fizemos foi dividir a nossa boundig box total, em duas separadas, isso não foi necessário na latitude, pq a longitude irá tratar de circundar os polos, pegando os pontos para nós.
PS: Esse caso da longitude tem que ser posto em um if, para mudar a query que iremos fazer a seguir e botar a outra boundig box nos parametros.
Nossa query final(ufa..)
Agora que computamos nossa Latitude min/max e Longitude min/max, iremos fazer um pré-filtro(que utilizará o poder dos indices) para depois realizar a query que tinhamos feito a princípio, aquela que verifica a distancia de cada ponto no DB. A diferença real aqui é que diminuimos a quantidade de pontos que iremos realizar essa verificação, sendo assim aprimoramos a nossa busca.
-- dado uma origem em O=(1.3963 rad, -0.6981 rad) latitude e longitude
-- temos 3 formas de fazer essa query:
-- obs: Lat e Lon são campos na nossa tabela
-- 1º combinando a query anterior com essa utilizando AND
SELECT * FROM LOCAIS WHERE
(Lat >= Latmin AND Lat <= Latmax) AND (Lon >= Lonmin AND Lon <= Lonmax)
AND
acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) <= r;
-- 2º o filtro na clausula where, utilizando HAVING na fórmula complexa
SELECT * FROM LOCAIS WHERE
(Lat >= Latmin AND Lat <= Latmax) AND (Lon >= Lonmin AND Lon <= Lonmax)
HAVING
acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) <= r;
-- 3º o filtro dentro de uma sub-query
SELECT * FROM (
SELECT * FROM LOCAIS WHERE
(Lat >= Latmin AND Lat <= Latmax) AND (Lon >= Lonmin AND Lon <= Lonmax)
) WHERE
acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) <= r;
-- Naquele caso especial da longitude no meridiano de 180º
-- só precisariamos add a outra bounding box na query
SELECT * FROM LOCAIS WHERE
(Lat >= Latmin AND Lat <= Latmax)
AND (
-- Lonmin < -π
((Lon >= (Lonmin+2*PI()) AND Lon <= PI())
OR
(Lon >= -PI() AND Lon <= Lonmax))
-- pra Lonmin > π é a mesma coisa, mas com os intervalos
-- demonstrados no tópico
)
HAVING
acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) <= r;
Conclusão
Esse artigo tinha ficado incrivelmente simples na minha cabeça, mas acabou sendo difícil resumir isso tudo de uma forma que todos pudessem entender.
Espero que tenham gostado de verdade, e que eu tenha atingido o meu objetivo, que era demonstrar de forma simples, como poderiamos realizar essa query sem nenhum erro.
O algoritmo de busca ja foi implementado em diversas linguagens como Javascript, PHP,PYTHON, C#, Clojure, Objective-C, e Swift. E o artigo que usei como base para fazer esse post se encontra aqui.
Espero ter ajudado e até a próxima ! õ7
